4x Squared Minus X Squared

Polynomial equation of degree two

This article is near algebraic equations of degree two and their solutions. For the formula used to find solutions to such equations, see Quadratic formula. For functions defined by polynomials of degree 2, see Quadratic function.

In algebra, a quadratic equation (from Latin quadratus  'square') is any equation that can be rearranged in standard form as

$${\displaystyle ax^{two}+bx+c=0}$$

where x represents an unknown, and a , b , and c represent known numbers, where a ≠ 0. (If a = 0 (and b ≠ 0) then the equation is linear, not quadratic, as there is no ${\displaystyle ax^{2}}$ term.) The numbers a , b , and c are the coefficients of the equation and may be distinguished by calling them, respectively, the quadratic coefficient, the linear coefficient and the constant or free term.^[1]

The values of x that satisfy the equation are called solutions of the equation, and roots or zeros of the expression on its left-hand side. A quadratic equation has at most two solutions. If at that place is but one solution, one says that information technology is a double root. If all the coefficients are existent numbers, in that location are either ii real solutions, or a single real double root, or two complex solutions that are complex conjugates of each other. A quadratic equation always has two roots, if circuitous roots are included; and a double root is counted for two. A quadratic equation can be factored into an equivalent equation

$${\displaystyle ax^{2}+bx+c=a(ten-r)(x-s)=0}$$

where r and southward are the solutions for ten.

The quadratic formula

$${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$$

expresses the solutions in terms of a, b, and c. Completing the foursquare is 1 of several ways for getting it.

Solutions to problems that tin be expressed in terms of quadratic equations were known as early on as 2000 BC.

Because the quadratic equation involves but one unknown, it is called "univariate". The quadratic equation contains just powers of x that are not-negative integers, and therefore information technology is a polynomial equation. In particular, information technology is a second-degree polynomial equation, since the greatest ability is 2.

Solving the quadratic equation [edit]

Figure 1. Plots of quadratic function y = ax ² + bx + c , varying each coefficient separately while the other coefficients are fixed (at values a = 1, b = 0, c = 0)

A quadratic equation with real or complex coefficients has two solutions, chosen roots. These two solutions may or may not be singled-out, and they may or may not be real.

Factoring past inspection [edit]

It may be possible to express a quadratic equation ax ² + bx + c = 0 every bit a product (px + q)(rx + s) = 0. In some cases, it is possible, by simple inspection, to determine values of p, q, r, and southward that make the two forms equivalent to one some other. If the quadratic equation is written in the second class, then the "Zero Gene Property" states that the quadratic equation is satisfied if px + q = 0 or rx + south = 0. Solving these two linear equations provides the roots of the quadratic.

For well-nigh students, factoring by inspection is the first method of solving quadratic equations to which they are exposed.^{[2] : 202–207} If one is given a quadratic equation in the class x ² + bx + c = 0, the sought factorization has the class (x + q)(x + s), and one has to discover two numbers q and s that add upward to b and whose product is c (this is sometimes called "Vieta'southward rule"^[3] and is related to Vieta's formulas). As an case, 10 ² + five10 + 6 factors as (10 + 3)(x + 2). The more general case where a does not equal 1 tin require a considerable endeavor in trial and error guess-and-check, assuming that it tin can be factored at all by inspection.

Except for special cases such as where b = 0 or c = 0, factoring by inspection only works for quadratic equations that have rational roots. This means that the nifty bulk of quadratic equations that arise in practical applications cannot exist solved by factoring past inspection.^{[2] : 207}

Completing the foursquare [edit]

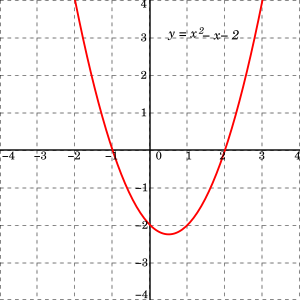
Figure 2. For the quadratic part y = x ² − x − 2, the points where the graph crosses the x -centrality, x = −ane and 10 = 2, are the solutions of the quadratic equation x ⁱⁱ − x − ii = 0.

The process of completing the foursquare makes use of the algebraic identity

${\displaystyle 10^{2}+2hx+h^{2}=(x+h)^{2},}$

which represents a well-defined algorithm that tin be used to solve whatsoever quadratic equation.^{[2] : 207} Starting with a quadratic equation in standard course, ax ² + bx + c = 0

1. Dissever each side past a , the coefficient of the squared term.
2. Subtract the constant term c/a from both sides.
3. Add the square of half of b/a , the coefficient of x , to both sides. This "completes the square", converting the left side into a perfect foursquare.
4. Write the left side equally a foursquare and simplify the right side if necessary.
5. Produce two linear equations past equating the square root of the left side with the positive and negative square roots of the right side.
6. Solve each of the 2 linear equations.

We illustrate use of this algorithm by solving 210 ² + 4ten − 4 = 0

${\displaystyle 2x^{2}+4x-4=0}$

${\displaystyle \ 10^{two}+2x-2=0}$

${\displaystyle \ x^{2}+2x=2}$

${\displaystyle \ x^{two}+2x+ane=two+1}$

${\displaystyle \left(x+i\right)^{2}=3}$

${\displaystyle \ 10+1=\pm {\sqrt {three}}}$

${\displaystyle \ 10=-1\pm {\sqrt {3}}}$

The plus–minus symbol "±" indicates that both ten = −i + √3 and x = −one − √three are solutions of the quadratic equation.^[4]

Quadratic formula and its derivation [edit]

Completing the square can be used to derive a general formula for solving quadratic equations, called the quadratic formula.^[5] The mathematical proof will now be briefly summarized.^[6] It tin hands be seen, past polynomial expansion, that the following equation is equivalent to the quadratic equation:

${\displaystyle \left(10+{\frac {b}{2a}}\right)^{two}={\frac {b^{2}-4ac}{4a^{2}}}.}$

Taking the square root of both sides, and isolating ten , gives:

${\displaystyle 10={\frac {-b\pm {\sqrt {b^{two}-4ac}}}{2a}}.}$

Some sources, particularly older ones, utilise alternative parameterizations of the quadratic equation such as ax ⁱⁱ + 2bx + c = 0 or ax ^two − 2bx + c = 0 ,^[7] where b has a magnitude one one-half of the more common one, maybe with opposite sign. These upshot in slightly different forms for the solution, merely are otherwise equivalent.

A number of culling derivations can be found in the literature. These proofs are simpler than the standard completing the square method, represent interesting applications of other frequently used techniques in algebra, or offer insight into other areas of mathematics.

A lesser known quadratic formula, as used in Muller'due south method provides the same roots via the equation

${\displaystyle ten={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac}}}}.}$

This can be deduced from the standard quadratic formula by Vieta's formulas, which assert that the product of the roots is c/a .

One belongings of this form is that information technology yields one valid root when a = 0, while the other root contains partition past cipher, considering when a = 0, the quadratic equation becomes a linear equation, which has one root. By dissimilarity, in this case, the more than common formula has a sectionalisation by zero for one root and an indeterminate form 0/0 for the other root. On the other hand, when c = 0, the more common formula yields 2 correct roots whereas this grade yields the nothing root and an indeterminate form 0/0.

Reduced quadratic equation [edit]

It is sometimes user-friendly to reduce a quadratic equation so that its leading coefficient is i. This is done by dividing both sides by a , which is e'er possible since a is non-zero. This produces the reduced quadratic equation:^[8]

${\displaystyle x^{2}+px+q=0,}$

where p = b/a and q = c/a . This monic polynomial equation has the same solutions as the original.

The quadratic formula for the solutions of the reduced quadratic equation, written in terms of its coefficients, is:

${\displaystyle x={\frac {1}{ii}}\left(-p\pm {\sqrt {p^{two}-4q}}\right),}$

or equivalently:

${\displaystyle x=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{ii}}\right)^{2}-q}}.}$

Discriminant [edit]

Figure 3. Discriminant signs

In the quadratic formula, the expression underneath the square root sign is called the discriminant of the quadratic equation, and is often represented using an upper case D or an upper case Greek delta:^[9]

${\displaystyle \Delta =b^{2}-4ac.}$

A quadratic equation with real coefficients tin can have either i or 2 distinct real roots, or two singled-out complex roots. In this case the discriminant determines the number and nature of the roots. There are 3 cases:

• If the discriminant is positive, and then there are two distinct roots

${\displaystyle {\frac {-b+{\sqrt {\Delta }}}{2a}}\quad {\text{and}}\quad {\frac {-b-{\sqrt {\Delta }}}{2a}},}$

both of which are real numbers. For quadratic equations with rational coefficients, if the discriminant is a square number, so the roots are rational—in other cases they may be quadratic irrationals.

• If the discriminant is zilch, then at that place is exactly one real root ${\displaystyle -{\frac {b}{2a}},}$ sometimes called a repeated or double root.

• If the discriminant is negative, then there are no existent roots. Rather, at that place are 2 distinct (non-real) complex roots^[10] ${\displaystyle -{\frac {b}{2a}}+i{\frac {\sqrt {-\Delta }}{2a}}\quad {\text{and}}\quad -{\frac {b}{2a}}-i{\frac {\sqrt {-\Delta }}{2a}},}$

which are complex conjugates of each other. In these expressions i is the imaginary unit of measurement.

Thus the roots are distinct if and just if the discriminant is non-zero, and the roots are real if and simply if the discriminant is not-negative.

Geometric estimation [edit]

Graph of y = ax ² + bx + c , where a and the discriminant b ² − 4ac are positive, with

• Roots and y -intercept in red
• Vertex and axis of symmetry in bluish
• Focus and directrix in pink

Visualisation of the complex roots of y = ax ² + bx + c : the parabola is rotated 180° about its vertex (orange). Its x -intercepts are rotated 90° around their mid-point, and the Cartesian airplane is interpreted as the circuitous plane (greenish).^[xi]

The part f(x) = ax ^two + bx + c is a quadratic role.^[12] The graph of any quadratic function has the same general shape, which is called a parabola. The location and size of the parabola, and how information technology opens, depend on the values of a , b , and c . As shown in Figure 1, if a > 0, the parabola has a minimum point and opens upward. If a < 0, the parabola has a maximum indicate and opens downward. The extreme point of the parabola, whether minimum or maximum, corresponds to its vertex. The ten-coordinate of the vertex will be located at ${\displaystyle \scriptstyle x={\tfrac {-b}{2a}}}$ , and the y-coordinate of the vertex may be found by substituting this ten-value into the function. The y-intercept is located at the point (0, c).

The solutions of the quadratic equation ax ⁱⁱ + bx + c = 0 represent to the roots of the office f(x) = ax ² + bx + c , since they are the values of x for which f(x) = 0. As shown in Effigy ii, if a , b , and c are existent numbers and the domain of f is the ready of real numbers, then the roots of f are exactly the x -coordinates of the points where the graph touches the x -axis. As shown in Figure 3, if the discriminant is positive, the graph touches the x -centrality at two points; if zero, the graph touches at ane point; and if negative, the graph does not touch the x -centrality.

Quadratic factorization [edit]

The term

${\displaystyle 10-r}$

is a cistron of the polynomial

${\displaystyle ax^{2}+bx+c}$

if and only if r is a root of the quadratic equation

${\displaystyle ax^{2}+bx+c=0.}$

It follows from the quadratic formula that

${\displaystyle ax^{ii}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(ten-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right).}$

In the special instance b ² = 4air-conditioning where the quadratic has but one distinct root (i.due east. the discriminant is cypher), the quadratic polynomial can be factored as

${\displaystyle ax^{two}+bx+c=a\left(10+{\frac {b}{2a}}\right)^{two}.}$

Graphical solution [edit]

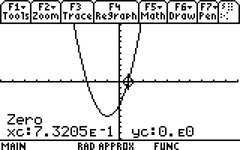
Figure 4. Graphing calculator computation of one of the two roots of the quadratic equation 2x ² + 4x − 4 = 0. Although the brandish shows only v pregnant figures of accuracy, the retrieved value of xc is 0.732050807569, authentic to twelve significant figures.

A quadratic office without real root: y = (x − 5)² + 9. The "iii" is the imaginary function of the 10-intercept. The real part is the x-coordinate of the vertex. Thus the roots are v ± iiii .

The solutions of the quadratic equation

${\displaystyle ax^{2}+bx+c=0}$

may be deduced from the graph of the quadratic function

${\displaystyle f(x)=ax^{2}+bx+c,}$

which is a parabola.

If the parabola intersects the x-axis in 2 points, there are two real roots, which are the x-coordinates of these ii points (too called x-intercept).

If the parabola is tangent to the x-axis, there is a double root, which is the x-coordinate of the contact point between the graph and parabola.

If the parabola does not intersect the x-axis, there are 2 complex conjugate roots. Although these roots cannot be visualized on the graph, their existent and imaginary parts can be.^[thirteen]

Let h and k be respectively the x-coordinate and the y-coordinate of the vertex of the parabola (that is the betoken with maximal or minimal y-coordinate. The quadratic function may be rewritten

${\displaystyle y=a(ten-h)^{ii}+yard.}$

Let d exist the distance between the indicate of y-coordinate twok on the axis of the parabola, and a point on the parabola with the same y-coordinate (meet the effigy; at that place are two such points, which give the same distance, considering of the symmetry of the parabola). And so the real function of the roots is h, and their imaginary function are ±d . That is, the roots are

${\displaystyle h+id\quad {\text{and}}\quad 10-id,}$

or in the case of the example of the figure

${\displaystyle 5+3i\quad {\text{and}}\quad 5-3i.}$

Avoiding loss of significance [edit]

Although the quadratic formula provides an verbal solution, the issue is not exact if real numbers are approximated during the computation, equally usual in numerical assay, where real numbers are approximated by floating betoken numbers (called "reals" in many programming languages). In this context, the quadratic formula is not completely stable.

This occurs when the roots have unlike order of magnitude, or, equivalently, when b ² and b ^two − fourair-conditioning are close in magnitude. In this case, the subtraction of ii nearly equal numbers will cause loss of significance or catastrophic cancellation in the smaller root. To avoid this, the root that is smaller in magnitude, r , tin can be computed as ${\displaystyle (c/a)/R}$ where R is the root that is bigger in magnitude.

A 2nd form of cancellation can occur between the terms b ² and 4ac of the discriminant, that is when the two roots are very close. This can lead to loss of up to half of right pregnant figures in the roots.^{[vii] [14]}

Examples and applications [edit]

The golden ratio is institute as the positive solution of the quadratic equation ${\displaystyle 10^{2}-x-1=0.}$

The equations of the circle and the other conic sections—ellipses, parabolas, and hyperbolas—are quadratic equations in 2 variables.

Given the cosine or sine of an angle, finding the cosine or sine of the angle that is half as large involves solving a quadratic equation.

The process of simplifying expressions involving the square root of an expression involving the square root of another expression involves finding the ii solutions of a quadratic equation.

Descartes' theorem states that for every four kissing (mutually tangent) circles, their radii satisfy a particular quadratic equation.

The equation given past Fuss' theorem, giving the relation amidst the radius of a bicentric quadrilateral's inscribed circle, the radius of its confining circle, and the distance between the centers of those circles, can be expressed as a quadratic equation for which the distance between the two circles' centers in terms of their radii is ane of the solutions. The other solution of the same equation in terms of the relevant radii gives the altitude betwixt the circumscribed circle'due south eye and the center of the excircle of an ex-tangential quadrilateral.

Disquisitional points of a cubic function and inflection points of a quartic function are found past solving a quadratic equation.

History [edit]

Babylonian mathematicians, every bit early on equally 2000 BC (displayed on Old Babylonian dirt tablets) could solve problems relating the areas and sides of rectangles. There is evidence dating this algorithm as far back every bit the Third Dynasty of Ur.^[15] In mod notation, the problems typically involved solving a pair of simultaneous equations of the form:

${\displaystyle x+y=p,\ \ xy=q,}$

which is equivalent to the argument that x and y are the roots of the equation:^{[16] : 86}

${\displaystyle z^{2}+q=pz.}$

The steps given by Babylonian scribes for solving the above rectangle problem, in terms of 10 and y, were as follows:

1. Compute half of p.
2. Square the event.
3. Subtract q.
4. Find the (positive) square root using a tabular array of squares.
5. Add together the results of steps (1) and (4) to requite 10 .

In modernistic note this means calculating ${\displaystyle x=\left({\frac {p}{2}}\correct)+{\sqrt {\left({\frac {p}{ii}}\right)^{two}-q}}}$ , which is equivalent to the modernistic day quadratic formula for the larger existent root (if any) ${\displaystyle x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}}$ with a = ane, b = −p , and c = q .

Geometric methods were used to solve quadratic equations in Babylonia, Egypt, Greece, China, and India. The Egyptian Berlin Papyrus, dating back to the Centre Kingdom (2050 BC to 1650 BC), contains the solution to a ii-term quadratic equation.^[17] Babylonian mathematicians from circa 400 BC and Chinese mathematicians from circa 200 BC used geometric methods of dissection to solve quadratic equations with positive roots.^{[18] [19]} Rules for quadratic equations were given in The Ix Chapters on the Mathematical Fine art, a Chinese treatise on mathematics.^{[19] [twenty]} These early on geometric methods do not announced to take had a full general formula. Euclid, the Greek mathematician, produced a more abstract geometrical method around 300 BC. With a purely geometric approach Pythagoras and Euclid created a general process to find solutions of the quadratic equation. In his work Arithmetica, the Greek mathematician Diophantus solved the quadratic equation, but giving only i root, even when both roots were positive.^[21]

In 628 AD, Brahmagupta, an Indian mathematician, gave the first explicit (although still not completely general) solution of the quadratic equation ax ² + bx = c equally follows: "To the absolute number multiplied by four times the [coefficient of the] foursquare, add the square of the [coefficient of the] heart term; the square root of the same, less the [coefficient of the] eye term, being divided by twice the [coefficient of the] square is the value." (Brahmasphutasiddhanta, Colebrook translation, 1817, page 346)^{[16] : 87} This is equivalent to

${\displaystyle x={\frac {{\sqrt {4ac+b^{ii}}}-b}{2a}}.}$

The Bakhshali Manuscript written in Bharat in the seventh century AD contained an algebraic formula for solving quadratic equations, every bit well equally quadratic indeterminate equations (originally of blazon ax/c = y ^{[ clarification needed : this is linear, not quadratic]}). Muhammad ibn Musa al-Khwarizmi (9th century), mayhap inspired by Brahmagupta,^{[ original research? ]} developed a set of formulas that worked for positive solutions. Al-Khwarizmi goes further in providing a full solution to the general quadratic equation, accepting one or two numerical answers for every quadratic equation, while providing geometric proofs in the process.^[22] He likewise described the method of completing the square and recognized that the discriminant must be positive,^{[22] [23] : 230} which was proven by his contemporary 'Abd al-Hamīd ibn Turk (Central Asia, 9th century) who gave geometric figures to prove that if the discriminant is negative, a quadratic equation has no solution.^{[23] : 234} While al-Khwarizmi himself did not have negative solutions, later Islamic mathematicians that succeeded him accepted negative solutions,^{[22] : 191} too as irrational numbers equally solutions.^[24] Abū Kāmil Shujā ibn Aslam (Egypt, 10th century) in particular was the kickoff to accept irrational numbers (often in the grade of a square root, cube root or fourth root) equally solutions to quadratic equations or as coefficients in an equation.^[25] The 9th century Indian mathematician Sridhara wrote down rules for solving quadratic equations.^[26]

The Jewish mathematician Abraham bar Hiyya Ha-Nasi (12th century, Kingdom of spain) authored the get-go European book to include the full solution to the general quadratic equation.^[27] His solution was largely based on Al-Khwarizmi'southward piece of work.^[22] The writing of the Chinese mathematician Yang Hui (1238–1298 Advertisement) is the start known one in which quadratic equations with negative coefficients of 'x' appear, although he attributes this to the earlier Liu Yi.^[28] Past 1545 Gerolamo Cardano compiled the works related to the quadratic equations. The quadratic formula covering all cases was first obtained by Simon Stevin in 1594.^[29] In 1637 René Descartes published La Géométrie containing the quadratic formula in the course we know today.

Advanced topics [edit]

Alternative methods of root calculation [edit]

Vieta'due south formulas [edit]

Graph of the difference betwixt Vieta's approximation for the smallest root of the quadratic equation x ² + bx + c = 0 compared with the value calculated using the quadratic formula

Vieta'south formulas (named after François Viète) are the relations

${\displaystyle x_{1}+x_{2}=-{\frac {b}{a}},\quad x_{1}x_{2}={\frac {c}{a}}}$

betwixt the roots of a quadratic polynomial and its coefficients. They upshot from comparing term past the relation

${\displaystyle \left(x-x_{i}\right)\left(x-x_{2}\right)=x^{2}-\left(x_{1}+x_{2}\right)x+x_{1}x_{2}=0}$

with the equation

${\displaystyle x^{two}+{\frac {b}{a}}x+{\frac {c}{a}}=0.}$

The commencement Vieta's formula is useful for graphing a quadratic function. Since the graph is symmetric with respect to a vertical line through the vertex, the vertex'southward x -coordinate is located at the average of the roots (or intercepts). Thus the 10 -coordinate of the vertex is

${\displaystyle x_{V}={\frac {x_{one}+x_{two}}{2}}=-{\frac {b}{2a}}.}$

The y -coordinate tin be obtained by substituting the above effect into the given quadratic equation, giving

${\displaystyle y_{5}=-{\frac {b^{2}}{4a}}+c=-{\frac {b^{2}-4ac}{4a}}.}$

These formulas for the vertex can also deduced directly from the formula (see Completing the foursquare)

${\displaystyle ax^{ii}+bx+c=a\left(\left(ten-{\frac {b}{2a}}\right)^{ii}-{\frac {b^{2}-4ac}{4a}}\right).}$

For numerical computation, Vieta's formulas provide a useful method for finding the roots of a quadratic equation in the case where one root is much smaller than the other. If |x _ii| << |ten _ane|, and so x _ane + x _two ≈ x ₁ , and nosotros take the estimate:

${\displaystyle x_{1}\approx -{\frac {b}{a}}.}$

The second Vieta's formula so provides:

${\displaystyle x_{ii}={\frac {c}{ax_{one}}}\approx -{\frac {c}{b}}.}$

These formulas are much easier to evaluate than the quadratic formula under the condition of one big and one minor root, because the quadratic formula evaluates the pocket-size root every bit the difference of two very nearly equal numbers (the case of big b ), which causes circular-off error in a numerical evaluation. The figure shows the difference between^{[ clarification needed ]} (i) a direct evaluation using the quadratic formula (authentic when the roots are near each other in value) and (two) an evaluation based upon the in a higher place approximation of Vieta'southward formulas (accurate when the roots are widely spaced). As the linear coefficient b increases, initially the quadratic formula is accurate, and the approximate formula improves in accurateness, leading to a smaller difference between the methods equally b increases. Notwithstanding, at some point the quadratic formula begins to lose accurateness considering of round off error, while the approximate method continues to better. Consequently, the difference between the methods begins to increase as the quadratic formula becomes worse and worse.

This situation arises commonly in amplifier design, where widely separated roots are desired to ensure a stable performance (see Step response).

Trigonometric solution [edit]

In the days earlier calculators, people would use mathematical tables—lists of numbers showing the results of adding with varying arguments—to simplify and speed up computation. Tables of logarithms and trigonometric functions were common in math and scientific discipline textbooks. Specialized tables were published for applications such as astronomy, celestial navigation and statistics. Methods of numerical approximation existed, called prosthaphaeresis, that offered shortcuts around fourth dimension-consuming operations such equally multiplication and taking powers and roots.^[30] Astronomers, especially, were concerned with methods that could speed upwardly the long series of computations involved in celestial mechanics calculations.

It is inside this context that nosotros may sympathize the development of means of solving quadratic equations past the aid of trigonometric substitution. Consider the following alternate form of the quadratic equation,

[1] ${\displaystyle ax^{2}+bx\pm c=0,}$

where the sign of the ± symbol is chosen so that a and c may both be positive. By substituting

[2] ${\displaystyle x={\sqrt {c/a}}\tan \theta }$

and so multiplying through past cos² θ , we obtain

[3] ${\displaystyle \sin ^{two}\theta +{\frac {b}{\sqrt {air-conditioning}}}\sin \theta \cos \theta \pm \cos ^{2}\theta =0.}$

Introducing functions of 2θ and rearranging, nosotros obtain

[4] ${\displaystyle \tan 2\theta _{n}=+ii{\frac {\sqrt {air-conditioning}}{b}},}$

[v] ${\displaystyle \sin 2\theta _{p}=-two{\frac {\sqrt {ac}}{b}},}$

where the subscripts n and p represent, respectively, to the use of a negative or positive sign in equation [1]. Substituting the two values of θ _north or θ _p plant from equations [4] or [5] into [2] gives the required roots of [one]. Complex roots occur in the solution based on equation [5] if the accented value of sin 2θ _p exceeds unity. The amount of effort involved in solving quadratic equations using this mixed trigonometric and logarithmic table await-upwards strategy was two-thirds the effort using logarithmic tables lone.^[31] Calculating circuitous roots would require using a different trigonometric grade.^[32]

To illustrate, permit us assume we had bachelor seven-place logarithm and trigonometric tables, and wished to solve the following to six-significant-figure accuracy:

${\displaystyle 4.16130x^{2}+9.15933x-11.4207=0}$

1. A 7-place lookup table might have but 100,000 entries, and computing intermediate results to vii places would generally require interpolation between adjacent entries.
2. ${\displaystyle \log a=0.6192290,\log b=0.9618637,\log c=1.0576927}$
3. ${\displaystyle 2{\sqrt {ac}}/b=2\times 10^{(0.6192290+1.0576927)/2-0.9618637}=1.505314}$
4. ${\displaystyle \theta =(\tan ^{-1}1.505314)/2=28.20169^{\circ }{\text{ or }}-61.79831^{\circ }}$
5. ${\displaystyle \log |\tan \theta |=-0.2706462{\text{ or }}0.2706462}$
6. ${\displaystyle \log {\sqrt {c/a}}=(i.0576927-0.6192290)/2=0.2192318}$
7. ${\displaystyle x_{1}=10^{0.2192318-0.2706462}=0.888353}$ (rounded to six significant figures)

${\displaystyle x_{ii}=-10^{0.2192318+0.2706462}=-3.08943}$

Solution for complex roots in polar coordinates [edit]

If the quadratic equation ${\displaystyle ax^{2}+bx+c=0}$ with existent coefficients has ii circuitous roots—the case where ${\displaystyle b^{2}-4ac<0,}$ requiring a and c to have the same sign as each other—then the solutions for the roots can be expressed in polar form every bit^[33]

${\displaystyle x_{1},\,x_{ii}=r(\cos \theta \pm i\sin \theta ),}$

where ${\displaystyle r={\sqrt {\tfrac {c}{a}}}}$ and ${\displaystyle \theta =\cos ^{-one}\left({\tfrac {-b}{two{\sqrt {ac}}}}\right).}$

Geometric solution [edit]

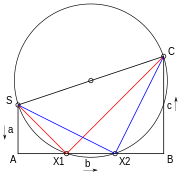
Figure half dozen. Geometric solution of ax ² + bx + c = 0 using Lill's method. Solutions are −AX1/SA, −AX2/SA

The quadratic equation may be solved geometrically in a number of ways. 1 way is via Lill's method. The 3 coefficients a , b , c are fatigued with right angles between them as in SA, AB, and BC in Figure vi. A circle is fatigued with the starting time and stop point SC every bit a diameter. If this cuts the center line AB of the iii so the equation has a solution, and the solutions are given past negative of the altitude along this line from A divided by the first coefficient a or SA. If a is 1 the coefficients may be read off straight. Thus the solutions in the diagram are −AX1/SA and −AX2/SA.^[34]

Carlyle circle of the quadratic equation ten ^two −sx +p = 0.

The Carlyle circle, named after Thomas Carlyle, has the property that the solutions of the quadratic equation are the horizontal coordinates of the intersections of the circumvolve with the horizontal axis.^[35] Carlyle circles have been used to develop ruler-and-compass constructions of regular polygons.

Generalization of quadratic equation [edit]

The formula and its derivation remain correct if the coefficients a , b and c are complex numbers, or more than mostly members of any field whose characteristic is non ii. (In a field of characteristic two, the chemical element 2a is zero and information technology is impossible to divide by information technology.)

The symbol

${\displaystyle \pm {\sqrt {b^{2}-4ac}}}$

in the formula should exist understood as "either of the two elements whose square is b ² − 4ac , if such elements exist". In some fields, some elements take no square roots and some accept 2; only zero has merely one square root, except in fields of characteristic 2. Fifty-fifty if a field does not contain a foursquare root of some number, there is e'er a quadratic extension field which does, and then the quadratic formula will always brand sense as a formula in that extension field.

Feature 2 [edit]

In a field of characteristic 2, the quadratic formula, which relies on 2 being a unit of measurement, does not concur. Consider the monic quadratic polynomial

${\displaystyle x^{2}+bx+c}$

over a field of feature 2. If b = 0, then the solution reduces to extracting a foursquare root, so the solution is

${\displaystyle x={\sqrt {c}}}$

and in that location is just one root since

${\displaystyle -{\sqrt {c}}=-{\sqrt {c}}+ii{\sqrt {c}}={\sqrt {c}}.}$

In summary,

${\displaystyle \displaystyle ten^{2}+c=(10+{\sqrt {c}})^{2}.}$

Come across quadratic residue for more data about extracting square roots in finite fields.

In the case that b ≠ 0, in that location are two singled-out roots, but if the polynomial is irreducible, they cannot be expressed in terms of foursquare roots of numbers in the coefficient field. Instead, define the 2-root R(c) of c to be a root of the polynomial x ² + ten + c , an element of the splitting field of that polynomial. One verifies that R(c) + 1 is likewise a root. In terms of the 2-root operation, the two roots of the (non-monic) quadratic ax ⁱⁱ + bx + c are

${\displaystyle {\frac {b}{a}}R\left({\frac {ac}{b^{ii}}}\correct)}$

and

${\displaystyle {\frac {b}{a}}\left(R\left({\frac {air-conditioning}{b^{2}}}\right)+1\correct).}$

For example, let a denote a multiplicative generator of the group of units of F _four , the Galois field of guild 4 (thus a and a + 1 are roots of x ² + ten + 1 over F ₄ . Considering (a + 1)² = a , a + ane is the unique solution of the quadratic equation x ² + a = 0. On the other manus, the polynomial ten ^two + ax + 1 is irreducible over F ₄ , merely it splits over F ₁₆ , where it has the two roots ab and ab + a , where b is a root of x ^two + ten + a in F _sixteen .

This is a special case of Artin–Schreier theory.

See also [edit]

• Solving quadratic equations with continued fractions
• Linear equation
• Cubic function
• Quartic equation
• Quintic equation
• Central theorem of algebra

References [edit]

1. ^ Protters & Morrey: "Calculus and Analytic Geometry. Starting time Grade".
2. ^ ^{a b c} Washington, Allyn J. (2000). Basic Technical Mathematics with Calculus, Seventh Edition. Addison Wesley Longman, Inc. ISBN978-0-201-35666-3.
3. ^ Ebbinghaus, Heinz-Dieter; Ewing, John H. (1991), Numbers, Graduate Texts in Mathematics, vol. 123, Springer, p. 77, ISBN9780387974972 .
4. ^ Sterling, Mary Jane (2010), Algebra I For Dummies, Wiley Publishing, p. 219, ISBN978-0-470-55964-2
5. ^ Rich, Barnett; Schmidt, Philip (2004), Schaum'due south Outline of Theory and Problems of Uncomplicated Algebra, The McGraw-Hill Companies, ISBN978-0-07-141083-0 , Chapter 13 §four.4, p. 291
6. ^ Himonas, Alex. Calculus for Business and Social Sciences, p. 64 (Richard Dennis Publications, 2001).
7. ^ ^{a b} Kahan, Willian (November 20, 2004), On the Toll of Floating-Bespeak Computation Without Extra-Precise Arithmetic (PDF) , retrieved 2012-12-25
8. ^ Alenit͡syn, Aleksandr and Butikov, Evgeniĭ. Concise Handbook of Mathematics and Physics, p. 38 (CRC Press 1997)
9. ^ Δ is the initial of the Greek word Διακρίνουσα, Diakrínousa, discriminant.
10. ^ Achatz, Thomas; Anderson, John Yard.; McKenzie, Kathleen (2005). Technical Shop Mathematics. Industrial Press. p. 277. ISBN978-0-8311-3086-two.
11. ^ "Complex Roots Made Visible – Math Fun Facts". Retrieved i October 2016.
12. ^ Wharton, P. (2006). Essentials of Edexcel Gcse Math/Higher. Lonsdale. p. 63. ISBN978-one-905-129-78-ii.
13. ^ Alec Norton, Benjamin Lotto (June 1984), "Circuitous Roots Made Visible", The College Mathematics Periodical, 15 (iii): 248–249, doi:ten.2307/2686333, JSTOR 2686333
14. ^ Higham, Nicholas (2002), Accuracy and Stability of Numerical Algorithms (2d ed.), SIAM, p. x, ISBN978-0-89871-521-7
15. ^ Friberg, Jöran (2009). "A Geometric Algorithm with Solutions to Quadratic Equations in a Sumerian Juridical Certificate from Ur Three Umma". Cuneiform Digital Library Journal. 3.
16. ^ ^{a b} Stillwell, John (2004). Mathematics and Its History (2nd ed.). Springer. ISBN978-0-387-95336-6.
17. ^ The Cambridge Ancient History Part 2 Early History of the Middle East. Cambridge University Press. 1971. p. 530. ISBN978-0-521-07791-0.
18. ^ Henderson, David Westward. "Geometric Solutions of Quadratic and Cubic Equations". Mathematics Department, Cornell University. Retrieved 28 April 2013.
19. ^ ^{a b} Aitken, Wayne. "A Chinese Archetype: The Nine Chapters" (PDF). Mathematics Section, California State University. Retrieved 28 April 2013.
20. ^ Smith, David Eugene (1958). History of Mathematics. Courier Dover Publications. p. 380. ISBN978-0-486-20430-7.
21. ^ Smith, David Eugene (1958). History of Mathematics, Volume 1. Courier Dover Publications. p. 134. ISBN978-0-486-20429-1. Extract of folio 134
22. ^ ^{a b c d} Katz, V. J.; Barton, B. (2006). "Stages in the History of Algebra with Implications for Pedagogy". Educational Studies in Mathematics. 66 (2): 185–201. doi:10.1007/s10649-006-9023-7. S2CID 120363574.
23. ^ ^{a b} Boyer, Carl B.; Uta C. Merzbach, rev. editor (1991). A History of Mathematics. John Wiley & Sons, Inc. ISBN978-0-471-54397-8.
24. ^ O'Connor, John J.; Robertson, Edmund F. (1999), "Standard arabic mathematics: forgotten brilliance?", MacTutor History of Mathematics annal, University of St Andrews "Algebra was a unifying theory which allowed rational numbers, irrational numbers, geometrical magnitudes, etc., to all be treated as "algebraic objects"."
25. ^ Jacques Sesiano, "Islamic mathematics", p. 148, in Selin, Helaine; D'Ambrosio, Ubiratan, eds. (2000), Mathematics Across Cultures: The History of Non-Western Mathematics, Springer, ISBN978-one-4020-0260-1
26. ^ Smith, David Eugene (1958). History of Mathematics. Courier Dover Publications. p. 280. ISBN978-0-486-20429-1.
27. ^ Livio, Mario (2006). The Equation that Couldn't Exist Solved. Simon & Schuster. ISBN978-0743258210.
28. ^ Ronan, Colin (1985). The Shorter Scientific discipline and Civilization in Prc. Cambridge University Printing. p. 15. ISBN978-0-521-31536-4.
29. ^ Struik, D. J.; Stevin, Simon (1958), The Principal Works of Simon Stevin, Mathematics (PDF), vol. II–B, C. V. Swets & Zeitlinger, p. 470
30. ^ Ballew, Pat. "Solving Quadratic Equations — By analytic and graphic methods; Including several methods you may never have seen" (PDF). Archived from the original (PDF) on nine April 2011. Retrieved 18 April 2013.
31. ^ Seares, F. H. (1945). "Trigonometric Solution of the Quadratic Equation". Publications of the Astronomical Lodge of the Pacific. 57 (339): 307–309. Bibcode:1945PASP...57..307S. doi:x.1086/125759.
32. ^ Aude, H. T. R. (1938). "The Solutions of the Quadratic Equation Obtained by the Aid of the Trigonometry". National Mathematics Magazine. 13 (three): 118–121. doi:10.2307/3028750. JSTOR 3028750.
33. ^ Simons, Stuart, "Alternative approach to circuitous roots of real quadratic equations", Mathematical Gazette 93, March 2009, 91–92.
34. ^ Bixby, William Herbert (1879), Graphical Method for finding readily the Real Roots of Numerical Equations of Any Degree, West Bespeak N. Y.
35. ^ Weisstein, Eric West. "Carlyle Circumvolve". From MathWorld—A Wolfram Web Resource . Retrieved 21 May 2013.

External links [edit]

• "Quadratic equation", Encyclopedia of Mathematics, Ems Press, 2001 [1994]
• Weisstein, Eric W. "Quadratic equations". MathWorld.
• 101 uses of a quadratic equation Archived 2007-11-10 at the Wayback Auto
• 101 uses of a quadratic equation: Part Ii Archived 2007-10-22 at the Wayback Machine

4x Squared Minus X Squared,

Source: https://en.wikipedia.org/wiki/Quadratic_equation

Posted by: harttaboure.blogspot.com

Share this post